考研数学中概率论与数理统计占到22%，两个大题三个小题，约34分。学习该科的重心是运用数学思维，并结合高数中的微积分等知识解决概率相关问题。下面是一些复习建议，大家重视起来做好复习也有机会把概率论部分的分全部拿到手的。

一、容易混淆的数学概念

①对立事件和互不相容（互斥）事件

通过定义可以发现：对立事件强调一个事件本身与其对立事件的并集等于总的样本空间,且一者发生则另一者必然不发生；而互不相容（互斥）事件，只强调一者发生则另一者必然不发生，即对立必然互斥，互斥不一定会对立。可以看出对立事件属于一种特殊的互斥事件。

在运用概念解题时，一定要注意两者的区别。

②互不相容（互斥）事件与独立事件

两者的不同点大致有如下三点 ：

第一 ，针对的角度不同．前者是针对能不能同时发生 ，即两个互不相容（互斥）事件是指两者不可能同时发生 ；后者是针对有没有影响，即两个相互独立事件是指一个事件发生对另一个事件发生的概率没有影响(注意：不是一个事件发生对另一个事件发生没有影响 )。

第二，试验的次数不同。前者是一次试验下出现的不同事件，后者是两次或多次不同试验下出现的不同事件。

第三 ，概率公式不同，若A与B为互斥事件，则有概率加法公式P(A+B)=P(A) + P(B)若A与B不为互斥事件，则有公式P(A + B) = P(A) + P(B)- P(AB)；若A与B为相互独立事件 ，则有概率乘法公式P(AB)= P(A)P(B)。

③条件概率公式与概率的乘积公式

已知事件A发生的条件下事件B发生的概率为条件概率，而概率的乘积公式中所涉及的事件没有“已发生”这个前提，两者的关系为：

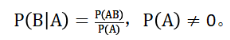
④随机变量的独立性与不相关性

如果两个随机变量独立，就是说它们之间没有任何关系；若不相关只是说明它们之间不具有线性关系，但是可以有别的关系，所以不一定相互独立。即独立一定不相关，不相关不一定独立。

二、解题技巧、方法的掌握和运用

数学模型的建立，是解决数学问题的关建。故学生应该在概率论的学习过程中，建立自己的知识体系，概括出重要的概率模型，并运用其解决概率问题。

三、典型例题、习题、真题的反复计算

俗话说，好脑子不如烂笔头，在学习概率的过程中，不要过分的、盲目的相信自己，只有你动笔写的时候才会发现自己的知识盲点，因此例题、习题的多次计算是必不可少的。我们深知做真题才是最逼近考场考试的，故多次刷真题是提升自我的一种方式。